No lo puedo resistir, me surge a flor de piel. En un nuevo Día Internacional de la(s) Matemática(s) inevitablemente pienso en qué significa que el principal evento a nivel mundial de visibilización de esta disciplina no represente un hecho histórico, como ocurriría en cualquier otro caso, sino más bien un juego de fechas del icónico número Pi. Me pregunto: ¿qué decidimos mostrar como comunidad de investigadores, de aficionades y de docentes cuando sugerimos ante la UNESCO ser recordades vía la relación entre el diámetro de un círculo y su circunferencia?

Intentando buscar alivio a mi evidente frustración, escribo este texto, con la esperanza de que algún día despertemos de este sueño. Ya lo he intentado anteriormente, contando por ejemplo cómo el camino de Pi a la fama se construyó gracias al trabajo de grandes mentes que pensaron en múltiples problemas por más de dos milenios, como ser el diseño de artefactos, las teorías científicas y la codificación de mensajes. Sin embargo, esos nombres quedan injustamente en el olvido, eclipsados por Pi. También lo intenté contando la infraestructura invisible que la comunidad matemática construyó para que hoy nosotres podamos, entre otras cosas, conocer el pronóstico del tiempo y usar internet en nuestro día a día. En esta oportunidad, intentaré algo menos sutil que antes: me gustaría poder derrocar los mitos que nos han estado contando, la cultura del número que nos han inculcado, encerrada en lo “útil” y lo “bello” pero que por algún motivo aún nos sigue resultando ajeno. Comienzo entonces por el mito con el que más me he enfrentado en mi vida:
¿Cuán hábiles son les matemátiques haciendo cuentas?
Me pasa realmente muy seguido, incluso entre gente muy cercana, que creen que soy capaz de hacer cálculos prodigiosos. Acepté que estoy condenado a escuchar el “vos que sos matemático, haceme esta cuenta” cada vez que haya comentado de mi especialidad, generalmente al presentarme en un nuevo grupo de gente, o el “¿Qué pasó? Hice la cuenta más rápido que vos”, dejando de lado lo competitivo que puedo llegar a ser. Después de respirar profundo y sonreír, mi respuesta suena más o menos así: “las cuentas ya las hace la calculadora (no vivimos en el siglo XIX)”.
Es cierto, les matemátiques ya no hacemos cuentas, de la misma manera en que ya poca gente recuerda los números de teléfono o cumpleaños de todas sus amistades, todo gracias a la automatización. Probablemente una persona que trabaje en contabilidad, finanzas o ingeniería sea más diestra con las cuentas que quien lo haga en matemática, pero más que nada por comodidad. Por supuesto, es una habilidad que puede ser innata o incluso entrenarse, pero no es un requisito para hacer matemática. Les calculistas mentales y calculadoras humanas fueron realmente útiles hasta antes de la creación de la computadora, pero en la actualidad esta actividad está más asociada a un deporte y al entretenimiento que a nuestra profesión.

Pero entonces, ¿por qué hacer cuentas está asociado con saber matemática? Aunque esto no quede muy bien explicado en la educación formal porque se prioriza la memorización, lo que sí nos interesa saber es cómo funcionan, cuáles son sus propiedades, qué representan sus resultados y cómo se pueden definir “nuevas” cuentas que nos sean útiles para resolver otros problemas. Y hablando de cuentas...
¿Es 2+2 siempre 4?
En varias oportunidades he escuchado la frase “en esta situación dos más dos no necesariamente vale cuatro”, como un caso particular del clásico “esto no es matemática”, dando a entender que cuando hablamos en términos matemáticos ya todo está ordenado, rígido, preciso, sin posibilidad de argumentar otras alternativas. Y es que la educación formal de la matemática la hemos recibido de esa manera en que 2+2 es 4, por lo tanto no tiene sentido discutirlo ¿o sí? De hecho, en más de una oportunidad el arte popular se ha encargado de decirnos que esto puede ser discutido, siempre y cuando lo que digamos tenga sentido dentro de un contexto apropiado. Tal es el caso de una canción que propone que a cada suma le hagamos un sustraendo. En tal caso, 2+2 sería 3. O bien, el caso del niño que afirmaba que 2+2 valía 22, porque no era capaz de ver al 2 como una abstracción de cantidad, sino como un objeto real que se ubicaba junto a otro de su misma especie. Entonces, en ese contexto, tiene sentido decir por ejemplo que 2+2+2=222. Pero yendo a casos menos excepcionales, podemos pensar en un reloj de agujas que en vez de tener 12 horas marque solamente 3. Por lo que, si a la hora 2 le sumo 2 horas más, entonces la respuesta es 1… ¿ahora ven por qué no hay que pedirnos que hagamos cuentas?
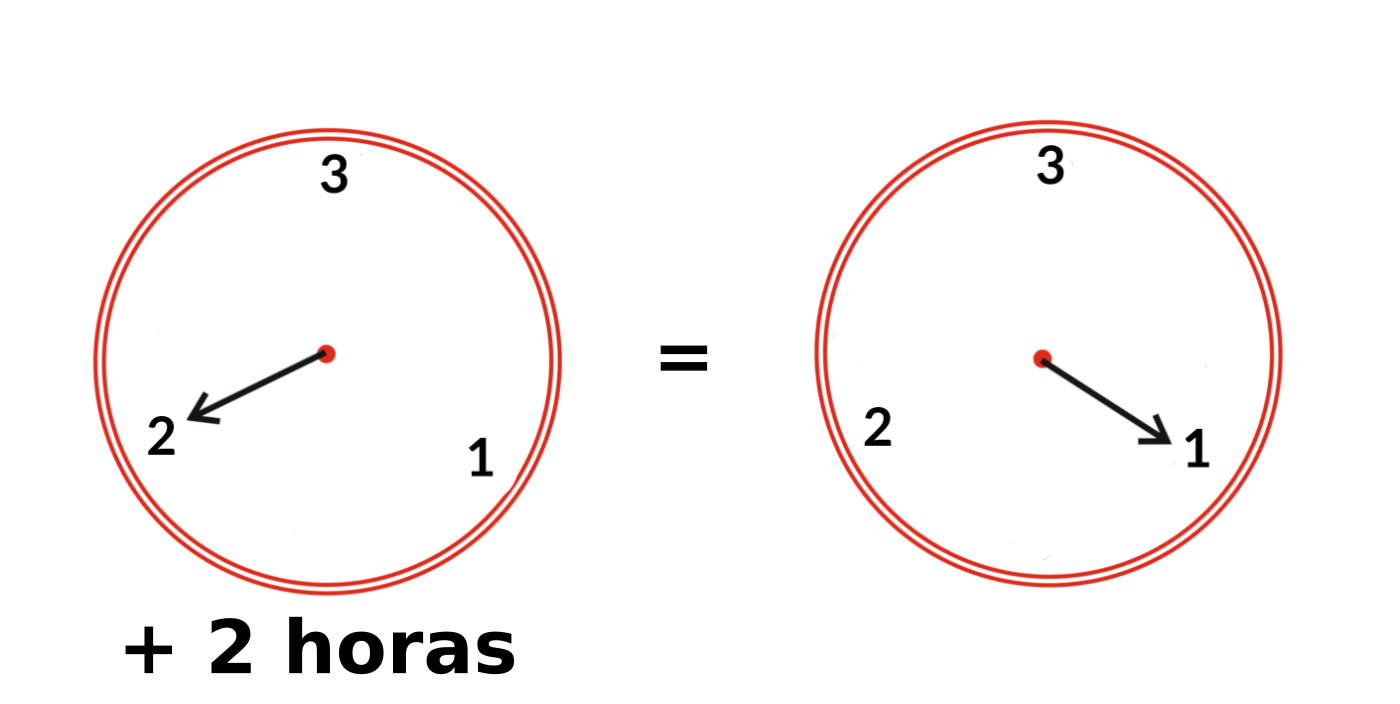
Todas estas situaciones no son ajenas a la labor matemática. Al primer caso se lo puede identificar como un tipo de “suma trasladada”, donde todo funciona como lo que conocemos, sólo que “corrido” un lugar. En el segundo caso a tal operación no la llamamos suma, sino concatenación y aparece naturalmente en estructuras del álgebra. El tercer caso se trata de la aritmética modular o “del reloj”, y forma parte de, por ejemplo, los fundamentos teóricos detrás de la criptografía.
Está claro entonces que el mito de la matemática rígida es, por lo menos, exagerado. Simplemente se trata de ponerse de acuerdo en el contexto de aplicación. Pero entonces la verdadera pregunta es, ¿por qué seguimos pensando que 2+2 debe ser 4? ¿No es más conveniente enseñar a pensar cuándo 2+2 debe ser 4? Es en esta pregunta donde aparece la matemática que realmente queremos comunicar, la que ejercita el razonamiento crítico para poder buscar soluciones menos convencionales para resolver un problema. Es la matemática que aparece por ejemplo en la búsqueda de soluciones para las minorías sociales, de la gente que no accede a la “estructura del 2+2=4” que las mayorías consideran verdadera y única, por su género, color de piel, orientación sexual o nación, y tiene que buscar otras respuestas más compatibles con su contexto de vida para ser felices.
Concretamente, hasta hace tan sólo unas décadas, era indiscutido que una familia comenzaba con un papá y una mamá. Cualquier otra situación estaba mal. ¿Cuán fácil hubiera sido aceptar que se pueden conformar otros tipos de familias si desde la infancia nos hubieran enseñado a pensar cuándo 2+2 puede ser 4 y cuándo no. Sería el “ejercicio fácil” para aprender a pensar de una manera distinta, y que nos ayude a vivir mejor entre todes. Y con esta manera de ver la matemática, vale ahora preguntarse:
¿Es la matemática objetiva y ajena a la realidad?
Una vez más, es una pregunta a la que la mayoría diría que sí casi con total seguridad, porque aunque el conocimiento matemático pueda ser usado para el bien o para el mal, la matemática en realidad no se mancha. Este es un razonamiento aplicable a cualquier tipo de conocimiento, pero la matemática tiene otro as bajo la manga, y es que su acción sobre la realidad está inevitablemente intermediada por otras disciplinas, como podrían ser la física, la computación o la economía.
Ahora bien, la búsqueda de conocimiento no está motivada por la inocente curiosidad humana: hay tendencias, intereses, guerras e inversiones en juego. Si hay algo que nos enseñó la pandemia, es que tenemos muy poco tiempo para determinar qué conocimiento debemos obtener para lograr nuestros objetivos, y que también debemos decidir qué organizaciones son las más aptas para el trabajo. Por otro lado también existe el conocimiento “malintencionado”, motivado por otros intereses.
Bajo esta perspectiva, hablar de “objetividad” suena a querer tirar la pelota afuera, algo que puede servir para sacarnos de encima la cuestión, pero oculta peligrosamente el verdadero problema de fondo: ¿con qué intencionalidad y para quién generamos conocimiento? Suponiendo que aceptamos esta “neutralidad” del conocimiento, ¿es posible concederle también esta “neutralidad” a la comunidad generadora de ese conocimiento, considerando su lugar en la sociedad y cómo interactúa con ella? ¿Debemos hacerlo? Lamentablemente no hay una respuesta para todo esto. Como tampoco queda claro el lugar que ocupa la matemática en la generación de conocimiento, adelantando un poco la respuesta a la siguiente pregunta:
¿Es la matemática un lenguaje? ¿Un tipo de arte? ¿Una ciencia?
El argumento principal que se usa para decir que la matemática no es una ciencia es la que dice que “no estudia la realidad”, que no habla sobre verdades del mundo sino de verdades lógicas y que sus objetos forman parte de un universo que un tal Platón nombró como “el de las ideas”. En este universo, las opiniones, las emociones, lo contextual, hasta lo temporal quedaba fuera. La concepción de que las matemáticas son eternas es algo bastante extendido en el saber popular. Incluso la Iglesia dio a entender alguna vez que en este universo atemporal es donde reside Dios. Así es como surgió la idea de que hay una matemática pura, cercana a lo divino, separada de lo mundano. Pero era imposible ignorar a las otras matemáticas, las que nos hacían la vida más fácil, práctica y disfrutable: la música, la física, la estadística, la contabilidad. Aunque esas estaban “contaminadas de realidad”, fue su utilidad la que les dio un lugar en la Historia.

Cuando Galileo Galilei dijo: “Las matemáticas son el lenguaje con el que Dios ha escrito el universo”, la palabra lenguaje quedó resonando en nuestros oídos hasta el día de hoy (la divinidad ya estaba sobreentendida) y con el tiempo esta metáfora quedó como una definición posible para la disciplina (la divinidad a esta altura es irrelevante). Pero por otro lado, hubo gente que se preguntaba cuál era la necesidad de tener en este lenguaje “palabras” que tal vez nunca encontrarían su contraparte en el universo. Ante este vacío exterior, buscaron la respuesta en su interior al calificarlas de artísticas, como una suerte de “supercalifragilisticoespialidoso”.
Todas estas interpretaciones, junto a otros factores, fueron generadoras de lo que se conoce como la crisis de los fundamentos de la matemática. Si bien hasta el día de hoy no está del todo resuelta, este debate dio lugar al paradigma que rige actualmente, una suerte de equilibrio inestable donde de alguna manera conviven estas tres miradas, entre otras. El hecho es que luego de más de 100 años aún nos estamos preguntando cómo llamar a la matemática...
¿Cómo se dice: en plural o en singular?
Habrán notado que en este texto y otros suelo usar el singular para nombrar a la matemática. Hay que aclarar que si bien ambas son correctas, en gran parte del mundo de habla hispana lo que predomina es el plural. Este es el motivo por el cual se podría decir que la RAE lo considera como la “versión oficial”. Dicho esto, desde una mirada lexicográfica todavía queda un análisis pendiente, siendo que en otros idiomas lo que predomina es el singular.
Es evidente que la pluralidad surge de su historia, es decir, de entender a la matemática como una colección de diferentes saberes. Pero así como ocurrió con otras disciplinas científicas y con la ciencia misma, se utiliza el singular como símbolo de integración de los diferentes saberes de una misma temática. Por ejemplo, en física tenemos la relatividad, la cuántica, el electromagnetismo, la termodinámica, etc, que hoy entendemos forman parte de un mismo cuerpo de saberes. En el caso de la matemática, luego de la crisis de los fundamentos de la matemática, la unificación formó parte de los objetivos de David Hilbert en su exposición de 1900.

Este concepto de unificación y de que la comunidad matemática argentina se sienta parte de la científica, hace que por estos lados la matemática se perciba como una ciencia, y es en ese contexto que aparece el uso del singular. El hecho de que aún no quede claro si hay que usar plural o singular justamente tiene que ver con que todavía no fuimos capaces de resolver esta última pregunta: ¿Qué es la matemática? Pero este interrogante lo voy a dejar para otro momento.
