Emile Cartan estaba harto de cómo se enseñaba matemática en la Universidad. Los métodos clásicos no eran suficientes para que él pudiera compartir a gusto sus conocimientos, sobre todo porque la disciplina había cambiado sus fundamentos en las últimas décadas y la generación que debía haber asimilado esos cambios había caído en la Primera Guerra Mundial. No era la primera vez que su amigo André Weil escuchaba este reclamo: era una frustración compartida por todo su grupo de ex-compañeros de la École Normale Supérieure de París, que en ese momento estaban a cargo de los cursos de matemática de nivel superior. Es por eso que, para terminar de una vez por todas con esta situación, le propuso convocarlos para reescribir los textos de algunas cursadas. Aunque ellos no lo sabían aún, este fue el origen de lo que hoy se conoce como el grupo Bourbaki.

Bourbaki es un nombre extraño para un grupo de matemáticos franceses, ya que no hay matemáticos reconocidos con ese apellido ni su origen es francés. Al parecer el apellido proviene de un general francés, Charles Denis Sauter Bourbaki, hijo de un coronel griego. Pero la referencia más asentada asociada al grupo es la de una anécdota, recordada por André Weil en su libro, que vivieron como estudiantes de la ENS en 1923: uno de sus compañeros, Raoul Husson, se presentó en un seminario con una barba falsa para dar una demostración del “Teorema de Bourbaki”, un sinsentido de razonamientos e intencionalmente incomprensible. Quien haya ido a alguna sesión de un congreso de matemática alguna vez sin tener idea de lo que se está hablando, seguramente sabe a lo que me refiero. Y quien no, también.

El grupo original conformado en 1935 se componía de Henri Cartan, Claude Chevalley, Jean Coulomb, Jean Delsarte, Jean Dieudonné, Charles Ehresmann, René de Possel, Szolem Mandelbrojt, André Weil, todos ellos ex-estudiantes de la ENS, con excepción de Mandelbrojt (para quien sabe de fractales, el tío de Benoit). Además de su particular carisma, André Weil ya había encarado una propuesta similar en la India, por lo tanto era el más apto para liderar el proyecto.
El objetivo era el de realizar una publicación elemental de Análisis que sirviera tanto de apunte de estudio para las nuevas generaciones como fuente de rigurosidad y detalle para el dictado de cursos, utilizando los métodos de demostración que el estudio de la lógica había reforzado. Pero pronto se dieron cuenta de que al hacerlo así estarían en contra de otra de las premisas del grupo: evitar la división extrema de las especialidades en matemática. Por lo que el proyecto se transformó en varias series de varios volúmenes sobre temas como Teoría de Conjuntos, Álgebra, Topología, Espacios Vectoriales, Integración e incluso Historia de la Matemática. Notando que tamaño plan acapararía más de una vida, y que la idea era que existiera una renovación constante, André Weil propuso que los mayores de 50 años dejaran de formar parte del grupo para dar lugar a las nuevas generaciones, quedando de forma consulta si se los convocara.

El grupo sigue existiendo hasta el día de hoy bajo L'Association des Collaborateurs de Nicolas Bourbaki, creada en 1952. Pero, más allá de sus fundadores, no se conocen con certeza qué otres matemátiques la han compuesto. El humor y el secretismo forman parte de la identidad del grupo, por eso la necesidad de crear al personaje Nicolás Boubaki del “desaparecido” país europeo de Poldavia como autor de las publicaciones y luego a su familia. Los textos que hablan de un casamiento y fallecimiento de los personajes, en realidad hacen referencia a eventos internos o críticas que el grupo hizo en su momento. En ellas podemos encontrar múltiples referencias de humor absurdo a reconocidos objetos matemáticos y personalidades, jugando con palabras y reinterpretaciones. Esta identidad mística y humorística era clave para mantener al grupo unido a pesar de las discusiones que ocurrían puertas adentro.
La Segunda Guerra Mundial afectó a los Bourbaki, con André Weil escapando entre los países del norte de Europa y luego emigrando a EE.UU., pero la tenacidad y la amistad de sus integrantes hizo que la iniciativa se pudiera mantener en el tiempo. Para la década de 1960 ya era un grupo de influencia y una corriente de pensamiento dentro del mundo matemático, cuyo ideal era el de unificar toda la matemática a partir de la Teoría de Conjuntos. Dado que el proyecto nació desde una mirada docente, algunos “bourbakistas”, seguidores de esta filosofía, creyeron que podría ser aplicable incluso para la educación primaria, aunque el grupo no emitió ninguna opinión al respecto. En oposición a esta mirada están los anti-bourbakistas, que critican principalmente el formalismo excesivo en las demostraciones.
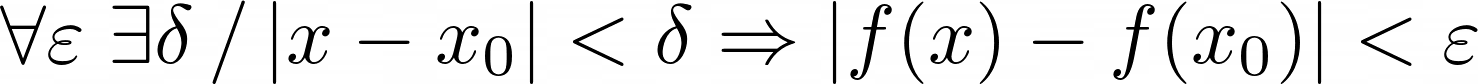
Los textos de Nicolás Bourbaki popularizaron los símbolos que se ven con extrañeza en la primera clase de matemática universitaria, como el “para todo”, el “existe” o el “conjunto vacío”. Pero lo que en realidad popularizaron fue la manera rigurosa, detallada y por sobre todo algebraica, abstracta y con la mayor generalidad posible de demostrar los teoremas en matemática. Su objetivo era erradicar a la geometría y reducirla al álgebra. Aunque obviamente no lo lograron, sí lo hicieron en el plano de las demostraciones, destronando así una manera de hacer contenido matemático que se venía arrastrando desde hacía más de dos milenios. Sin duda fueron quienes, para bien o para mal, marcaron una manera de trabajar que hoy se reproduce en cualquier escrito científico del área.
