Hoy se cumplen 100 años de la partida de unos de los personajes más particulares del siglo XX. Estoy hablando de Srinivasa Ramanujan, el último gran matemático autodidacta. Casi sin estudios formales y con un perfil místico, percibió una matemática que nosotros ni siquiera soñamos. Su manera de entenderla era más bien intuitiva. Mientras que hoy la mayoría de los académicos dependen de la lente del formalismo lógico para estudiarla, él podía andar libremente por ese mundo, encontrando por donde pasaba pepitas de oro en forma de identidades numéricas y ecuaciones. Nunca sabremos si realmente era un genio o la persona con más suerte en el mundo de la matemática.
Ramanujan nació en Erode, India, el 22 de diciembre de 1887, en el seno de una familia de la casta sacerdotal hindú, los brahamanes. Debido a que su padre trabajaba la mayor parte del día, su madre y sus abuelos se encargaron de cuidarlo y de enseñarle todas las tradiciones de su religión. Su primer encuentro con la matemática formal fue a los 11 años en la secundaria, aunque desde hace tiempo ya había empezado a sobresalir por su intelecto. Cuatro años más tarde, y habiendo leído bibliografía específica, ya era un experto geómetra y aportaba nuevos teoremas al área. Su apetito voraz por los libros de matemática avanzados se traducía en escritos con nuevas ideas y métodos de resolución de problemas y de cálculos de constantes. Su interés por la matemática era tan grande, que luego de haber ganado premios y reconocimientos durante su secundario, le ofrecieron una beca de estudios que más tarde perdería por estar sólo interesado en esta disciplina.
Luego de frustraciones académicas, decidió que su camino fuera el de la investigación independiente, aunque esto implique quedar sumido en la pobreza. Con el tiempo, Ramanujan empezó poco a poco a ser reconocido, pero su poca formación académica complicaba la comunicación con sus colegas. Varias veces afirmaba que sus resultados venían de inspiración divina y que “una expresión matemática no tiene significado para mí a menos que exprese un pensamiento de Dios”. Ante esta situación, algunos pensaron en él como un farsante, pero empezaron a reconocerlo al ver que era imposible que sus resultados le hubieran llegado por otros medios. Aún así, quedaba el problema de justificar y explicar correctamente sus ideas para que todo el mundo pudiera entenderlo, o al menos el mundo matemático académico.

Para ese entonces, la crisis de los fundamentos de la matemática iniciada a fines del siglo XIX había cambiado las reglas del juego sobre cómo justificar y explicar desarrollos matemáticos: ya no era suficiente dar a conocer una idea de forma intuitiva, la misma debía ir acompañada por una explicación con pasos lógicos coherentes en un lenguaje en el que Ramanujan nunca había podido formarse. Si Ramanujan hubiera nacido en Europa y 50 años antes, seguramente nos sería mucho más fácil ubicarlo entre los más grandes matemáticos de la historia, junto con Euler o Gauss, donde solemos olvidar que estos personajes nunca tuvieron la necesidad de justificar los resultados como lo hacemos hoy en día y que vivieron en una sociedad con mayores recursos que la de Ramanujan.
A pesar de todo esto, Ramanujan no se rindió. En 1913, con ayuda de los integrantes de la recién fundada Sociedad Matemática de la India, se puso en contacto con sus colegas británicos. Uno de ellos, Godrey Hardy, un reconocido matemático de la Royal Society, fue el único que le respondió. Aunque en un primer momento creyó también en un fraude, se convenció de que los teoremas de Ramanujan "deben ser verdad, porque, si no eran ciertos, nadie tendría la imaginación necesaria para inventárselos". Así que decidió escribirle y hasta viajar a la India, interesado por sus resultados y por la necesidad de tener pruebas de los mismos.
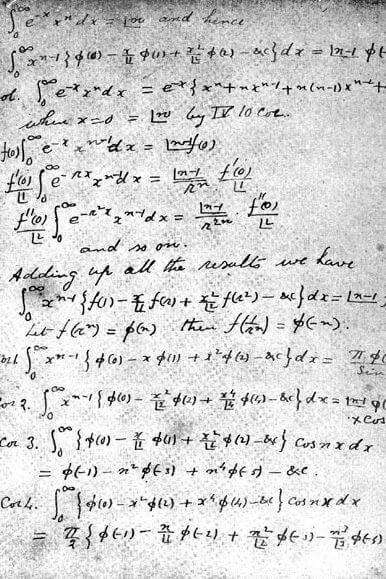
Un año más tarde, Ramanujan llegaba a Cambridge, invitado por Hardy y otro matemático de renombre, Littlewood. Los tres trabajaron juntos por casi 5 años, reformulando teoremas y dando nuevos resultados, que más tarde abrirían nuevas líneas de investigación en diferentes ramas de la matemática. Mientras Ramanujan era el principal autor de las ideas, Hardy y Littlewood se encargaban de enseñarle cómo debía transcribirlas en un lenguaje formal, o bien de hacerlo ellos mismos. De esta manera Ramanujan conseguía revalorizarlas dentro del mundo académico, llegando a obtener su doctorado y luego ser parte de la Royal Society, a pesar de su corta edad y de su origen indio, por aquel entonces, una colonia británica.
En 1919, Ramanujan decidió volver a la India. Su salud nunca había sido buena y, durante su estadía en Inglaterra, empeora considerablemente por no poder continuar su dieta tradicional religiosa y contraer tuberculosis. Falleció un día como hoy, pero de 1920, en Kumbakonam. En honor a él, en su país se declara la fecha de su nacimiento como el Día Nacional de la Matemática, pero su legado es conocido en todo el mundo. Muchos resultados hoy son clave para calcular con mucha precisión constantes como pi o e y valores de funciones que se usan tanto en investigaciones como desarrollos algorítmicos y resolución de problemas concretos.
