La verdad es que no sé por dónde empezar. Bah, sí sé, pero no quería ser tan brusco. Odio a Pi. Ya está, lo dije: odio a Pi. Odio que haya gente fan de Pi, que haya concursos a ver quién se sabe más decimales, que lo quieran escribir por todos lados, que se lo tatúen, que aparezca en la pizza y hasta en una clásica canción infantil. Tampoco es que banque a otros números, como Phi, i, e o el número primo más largo conocido hasta el momento. Pero al parecer Pi tiene algo especial, tan especial que la fecha elegida por la UNESCO para representar a la Matemática a nivel mundial, a sugerencia de la Unión Matemática Internacional, es el 14 de marzo, --03-14 en notación estándar.
Lo que no me cabe en la cabeza es la fama de Pi. No niego que pueda ser envidia. Probablemente sea el concepto más conocido de la matemática, superando incluso el Teorema de Tales, apodado como “la regla de tres simple”, porque llamar “teorema” a algo tan cotidiano es extraño. Otra ventaja que tuvo seguramente es que es conocido desde hace mucho. Hizo su primera aparición de joven, haya por la Revolución Neolítica, hace más de 6 mil años, ayudando a hacer vasijas, pero nadie sabía su nombre. Después lo convocaron para obras más grandes, como silos o anfiteatros, pero era sólo un número.
No obstante, algo empezó a cambiar cuando se unió a los filósofos griegos: Pitágoras, Platón, Aristóteles, Arquímedes, Euclides y muchos otros lo consideraron un ícono de la geometría. Pero lo discriminaron por su carater irracional y comenzaron a utilizar “dobles de riesgo” para sus trabajos. Algunos usaban directamente al 3, otros buscaban al 3,14 y los más especialistas sabían que con la fracción 22/7 tenían una buena performance a bajo costo. La venganza de Pi fue terrible: los griegos, amantes de los problemas geométricos, se preguntaron cómo construir un cuadrado con la misma área que un círculo. Tardamos dos mil años en descubrir que esto es imposible por la irracionalidad de Pi que los griegos ignoraron. Pero no nos adelantemos.
El reinado de los dobles de Pi se extendió por mucho tiempo, cada vez más parecidos al original, ayudados por la aparición de una nueva notación traída de oriente por Leonardo Fibonacci. Esta nueva manera de escribir números, usando la posición y los dígitos que conocemos hoy en día, fue clave para que la marca registrada de Pi estuviera por todos lados.
Se nota que Pi fue madurando a través del tiempo. A pesar de que nadie conocía aún su verdadera identidad, dejó de interesarle ser parte de las labores cotidianas. Entendió que el mundo aún no estaba preparado para conocerlo en su plenitud. Así que mientras esperaba por el momento oportuno, se dedicó a ser el principal asesor de sus dobles. De esa manera, los que antes competían por su puesto, se terminaron convirtiendo en sus principales predicadores, que profetizaban la venida del único Pi que siempre había existido.
Los años venideros trajeron consigo más desafíos para Pi. Si bien los dobles habían hecho su trabajo a la perfección, un resucitado Phi, ex-colega cuando estaba entre los griegos, había copado la escena natural, apareciendo en flores, caracoles y proporicones del cuerpo humano, convirtiéndose así en una de las estrellas del sector artístico del Renacimiento. La realidad era que Pi se había dedicado más a un perfil industrial. Siguió presentándose en versiones más precisas de poliedros, pero su gran aporte para este período fueron los engranajes, trabajando a la par de Leonardo Da Vinci. Algunos creen que esta idea estuvo basada en las poleas de Arquímedes, pero no hay pruebas claras. Lo cierto es que los dobles de Pi fueron claves: la cantidad de dientes que estas herramientas pueden tener está estrechamente ligada a sus aproximaciones cada vez más precisas.
Entrando en la época de los científicos naturales, Pi vio su oportunidad para empezar a forjar el puesto mítico que hoy tiene. La física y la matemática había avanzado lo suficiente para hacerse preguntas que estaban a la altura de su presencia y pudo darse a conocer a ellos sin prejuicios, recibiendo el nombre por el que hoy lo conocemos. Pero un nuevo contrincante había aparecido, tan potente como él, y que se estaba ganando el favor de arquitectos e ingenieros: e. Gracias a su rol en el problema de la catenaria, los humanos desarrollaron la capacidad de construir inmensos arcos y puentes sin que se destruyan a causa de su propio peso. La historia más adelante los convertiría en grandes compañeros.
Durante este tiempo se recrudece el trato entre los números racionales y Pi, y se suma e a la contienda. En aquel entonces la moda de los científicos era trabajar con funciones, y los números racionales tenían a los polinomios de su lado. Por su parte, Pi tenía a las funciones trigonométricas, mientras que e tenía a las exponenciales y las logarítmicas. La situación era la misma de siempre: si bien los humanos respetaban la potencia de estas extrañas funciones, estaban mucho más cómodos trabajando con polinomios. A menos que apareciera ese “bicho raro” al que llamaron i.
A medida que las investigaciones aumentaban, la tensión se tornaba insostenible: la aparición de i cada vez era más recurrente y, si bien cada uno tenía sus avances personales (las trigonométricas eran esenciales para entender ondas, mientras que las logarítmicas y las exponenciales se utilizaban para modelar fenómenos de crecimiento, ya sea en economía o biología), tantos los racionales como Pi y e sabían que la única solución era aunar fuerzas. Y con la ayuda de matemáticos de la talla de Leibniz, Cauchy, Euler y Gauss, entre muchos otros, lograron lo imposible: unir, lo que siempre se vio separado, en una sola fórmula.
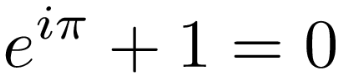
Ahí estaban todos reunidos para la foto: Pi, e, i, el 1, el 0, la suma, el producto, el exponente y el igual, en lo que se la conoce como la fórmula más bella de toda la matemática, principalmente porque en ella se eliminaron todos los prejuicios. Desde entonces, se siguieron reforzando vínculos de Pi y e asociados a sumas y productos infinitos de racionales icónicos, como los naturales o los números primos, y se reescribieron las funciones trigonométricas y las exponenciales como polinomios de términos infinitos. Esto derivó en muchas aplicaciones. mostrando que Pi junto con e son unos de los números claves para entender el mundo, pero Pi había consruido una gran imagen positiva gracias a sus dobles. Y aunque es cierto tiene feroces detractores, sabe que son aquellos con la mirada prejuiciosa de los griegos y aprendió a ignorarlos hace tiempo.
La historia de la fama de Pi podría terminar ahí, pero como ocurre en toda ciencia, la respuesta a una pregunta da nuevas preguntas, y este fue el caso del infinito. Al principio se llevó bien con todos lo números, pero tanto él como los demás sabían que no era uno de ellos. En el siglo XX se hizo un gran esfuerzo, reescribiendo toda la matemática para poder incluirlo a este selecto grupo, requiriendo desarrollar una notación sumamente rigurosa. Como efecto secundario de esta rigurosidad surgió la lógica, y luego la computación. Hoy, una vez más los números racionales dominan la labor principal, pero la comunicación de esta era sólo es posible gracias a que están Pi, e y sus dobles ayudándonos, en cada bit que mandamos por internet.
Habiéndoles contado esta historia, supongo que se estarán preguntando, ¿Por qué odio a Pi? Porque Pi no hizo nada de lo que les conté. Ni Pi, ni e, ni ningún número es el verdadero protagonista de esta historia. Simplemente fue un recurso narrativo. Los verdaderos protagonistas son y siempre serán los humanos: los filósofos, los científicos, los ingenieros y los artistas que estuvieron detrás para que todo esto pasara. Seguir alimentando la idea de que la matemática tiene ese espíritu lúdico, numerológico y por sobre todo ajeno a la realidad, mostrando que sus protagonistas son sus estructuras, lo único que genera es que su poder nos resulte ajeno, llevándonos a algunos a creer que son los constructores de la realidad o representantes de lo divino.
Sin embargo, este poder al que me refiero es muy nuestro, y con él hemos logrado cambiar nuestras vidas varias veces y de forma radical. Es el de pensar, de razonar, de madurar ideas y de utilizarlas para argumentar, para tener espíritu crítico, para defendernos de embaucadores y estafadores y para ser creativos y dar soluciones novedosas a los problemas que vivimos. Es el que da la libertad que quiere el artista, la utilidad que quiere el ingeniero, lo lúdico que quiere el docente y el poder de descubrir que quiere el científico. Es un poder que está dentro de nosotros, pero está en cada uno querer aprender a usarlo. Espero que en el día Internacional de la Matemática puedas empezar a descubrirlo. Es por eso que, te guste la matemática o no, también es válido decirte ¡Felíz día!
